二次函数经典题目:二次函数y=ax2+bx+c(a≠0)
二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2),且与x轴交点的横坐标为x1、x2,其中-2<x1<-1,0<x2<1,则下列结论:
①4a-2b+c<0,②2a-b<0,③a+c<1,④b2+8a>4ac.其中正确的是______.
解析:∵图象开口向下,则a<0,
∵图象对称轴在y轴左侧,则a,b同号,即b<0,
图象与y轴交于y轴正半轴,故c>0,
当x=-2时,函数值小于0,
即4a-2b+c<0,故①正确;
由-2<x1<-1,0<x2<1,可知对称轴x>-1
∴2a<b,即2a-b<0, ②正确
③开始尝试用c/a,x1*x2最大为0,最小-2,探索未果
利用特值:根据-2<x1<-1,0<x2<1,可以估算出两根的值,
例如x1=-1.5,x2=0.5,图象还经过点(-1,2),得出函数的解析,
解得:a=-8/3<-1,b=-8/3, c=2 a+c<0
④b2+8a>4ac.
根据③中计算结果,可以得出:b2+8a>4ac,
故④b2+8a<4ac,不正确.
也可以这么算 :
将点(-1,2)代入y=ax2+bx+c中,得a-b+c=2,即c=2-a+b,
由2a-b<0,则(2a-b)2>0,
即b2>-4a2+4ab,
∴b2+8a>8a-4a2+4ab=4a(2-a+b)=4ac,
故选:C.
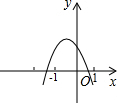

最新讨论