如图1是把一个任意四边形纸片的∠B折叠
如图1是把一个任意四边形纸片的∠B折叠,点B落在点B′,折痕为EF;图2是再折叠∠C,使F C沿F B′的方向落下,点C落在C′,折痕为FG.
(1)求∠EFG的度数;
(2)结合题意和(1)的结果,写出一个数学命题
解答:解:(1)∵∠BFE=∠EFB′,∠CFG=∠GFB′,
∴∠EFG=∠EFB′+∠GFB′=1/2∠BFB′+1/2∠CFB′=1/2(∠BFB′+∠CFB′)=90°;
(2)平角的两边分别以两条直线为折痕,向直线的同一侧折叠,折叠以后的两边重合,则两条折痕一定互相垂直,即:邻补角的角平分线互相垂直.
故答案是:邻补角的角平分线互相垂直.
∴∠EFG=∠EFB′+∠GFB′=1/2∠BFB′+1/2∠CFB′=1/2(∠BFB′+∠CFB′)=90°;
(2)平角的两边分别以两条直线为折痕,向直线的同一侧折叠,折叠以后的两边重合,则两条折痕一定互相垂直,即:邻补角的角平分线互相垂直.
故答案是:邻补角的角平分线互相垂直.
点评:本题考查了图形的翻折变换,以及角度的计算,难点是正确叙述(1),写出命题.
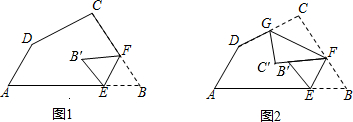

最新讨论