原来多项式可以用来玩涂色游戏

多项式不仅是课本上抽象的练习题。它们还有助于在一些令人意想不到的地方揭示数学结构。

 

2015年，诗人数学家June Huh帮助解决了一个50年前的问题。这个问题是关于一个叫做“拟阵”(matroids)的复杂的数学对象，它是由点、线和图片的组合而成。同时它也是一个关于多项式的问题——那些数学课上常见的可以把变量求不同幂次再求和的表达式。

有时你可能在学校里遇到多项式的合并、分解和简化的问题。例如，你也许记得x²  + 2xy + y²  = (x + y)² 。这是一个简洁的代数技巧，但是它到底有什么用处？多项式擅长于揭示隐藏结构，这个事实在Huh的证明中有着重要的作用。下面让我们用一个简单的例子来说明如何实现这一点。

假设这里有一个游戏要求将两组玩家安排在一张方桌上。为了防止他们作弊，需要避免同队的玩家坐在相邻的座位上。那么一共有多少种不同的安排方法？

游戏一开始，我们将玩家分为红色和蓝色两种。如图所示，假设先将一个红色玩家安排在图的上面的位置。

 

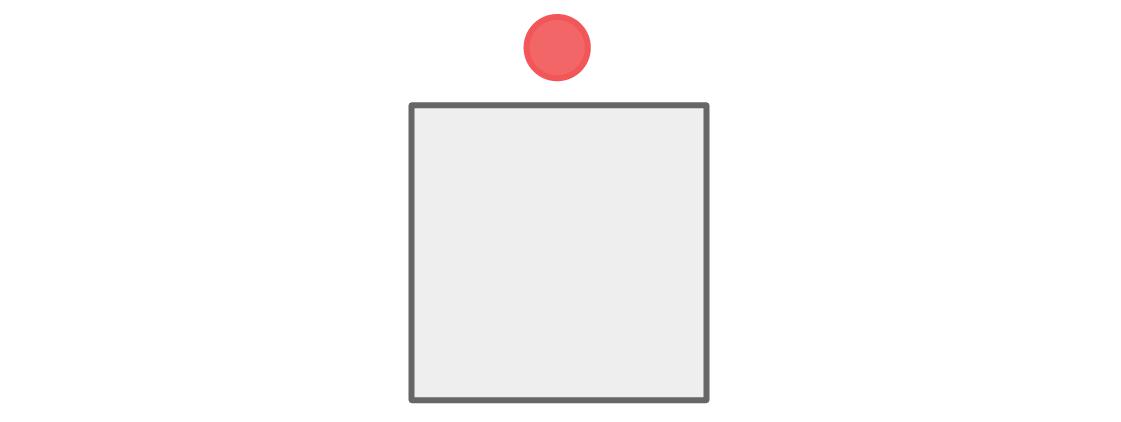
上面的位置左右各有一个相邻的座位，因此，为了满足我们的要求，这两个座位必须都安排给蓝色玩家。

 

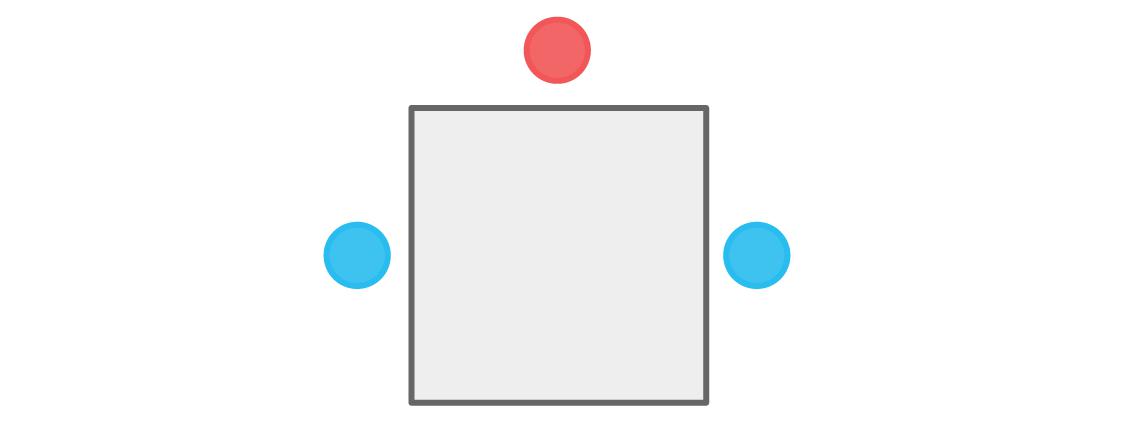
图的底部还剩下了一个和两个蓝色玩家相邻的位置，所以必须有一个红色的玩家坐在那里。

 

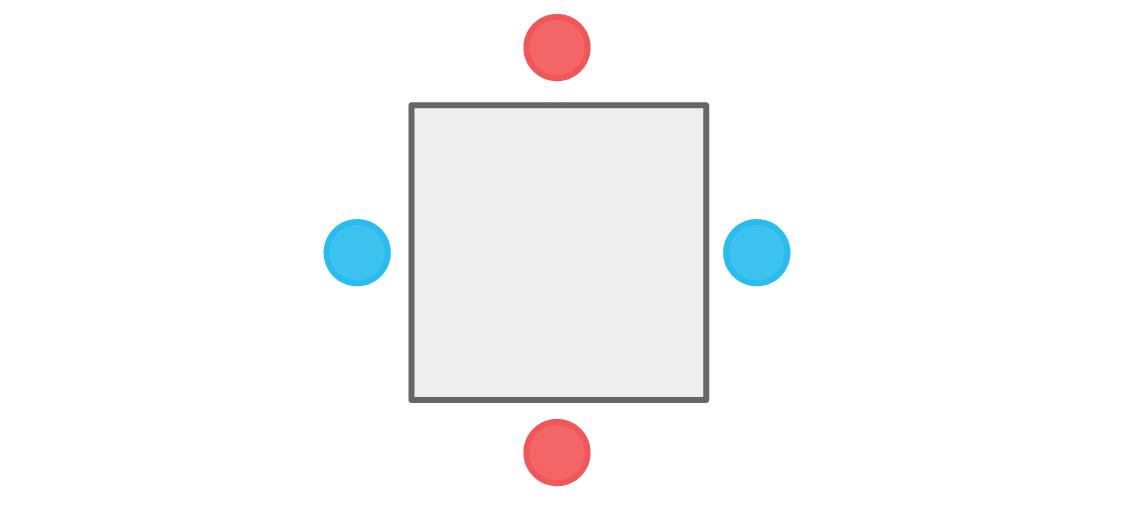
因为没有一个玩家坐在他队友的旁边，我们的限定的条件满足了。

我们也可以在游戏一开始的时候将一个蓝色玩家安排在上面。和上文相类似的推理可以得到下面的安排。

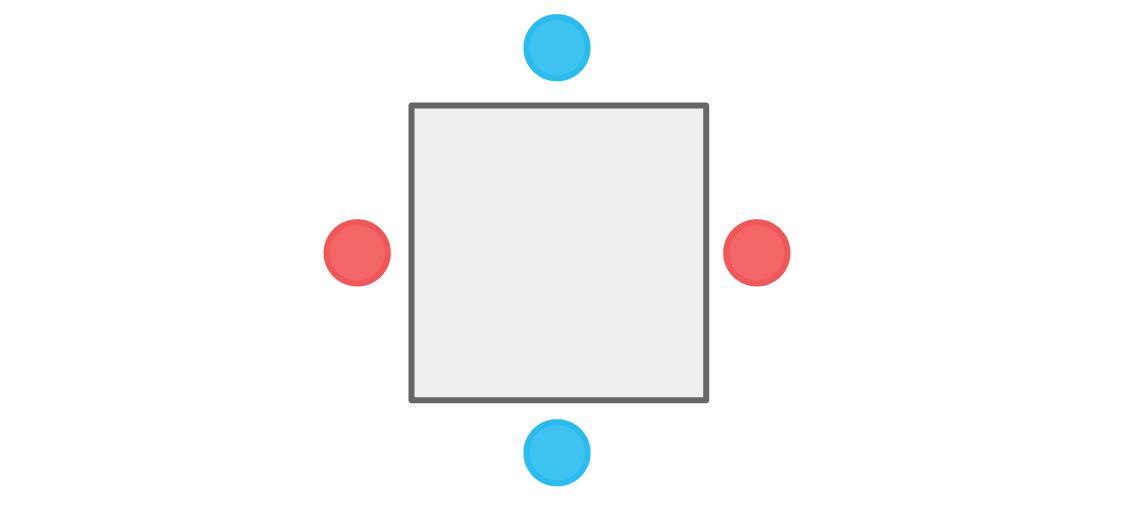
同样，没有一个玩家坐在他的队友的旁边。我们的约束条件满足了，所以这是另一种可能的安排方法。事实上，这个游戏只有两种可能的排座结果。一旦我们选定了上面位置的颜色，剩下座位的颜色也都决定好了。

有一种方法能让我们不用画出所有不同的座位图就可以知道只有两种安排座位的方法。让我们从上面开始：对那个座位我们有两种选择，红色或者蓝色。当我们做出这个选择的时候，它左边和右边的位置都只有一种选择（另一种颜色）。然后，对最下面的座位来说，也是只有一个选择：我们开始游戏的时候选择的颜色。通过运用“基本计算原理”，我们知道所有可能性的个数是每一种选择可能性数的乘积。这就得到了2 × 1 × 1 × 1 = 2一共两个座位，就像我们用图像的确定出来的一样。

现在，我们加入用其他颜色表示第三支队伍。想象现在有红色，蓝色和黄色三种玩家。如果相邻的座位不能安排同样颜色的玩家，那么有多少种不同的安排方式？画出所有的可能性可能会需要很多的图像，所以让我们改用计算参数试试。

现在上面的位置有三种颜色可以选择。做出选择之后，我们就可以为左右两个位置选择剩下两个颜色中的任意一个。

那么方桌下方的座位会发生什么？人们很容易说最后一个位置只有一种选择，因为它左右都有相邻的座位。但你有没有发现其中的问题？

 

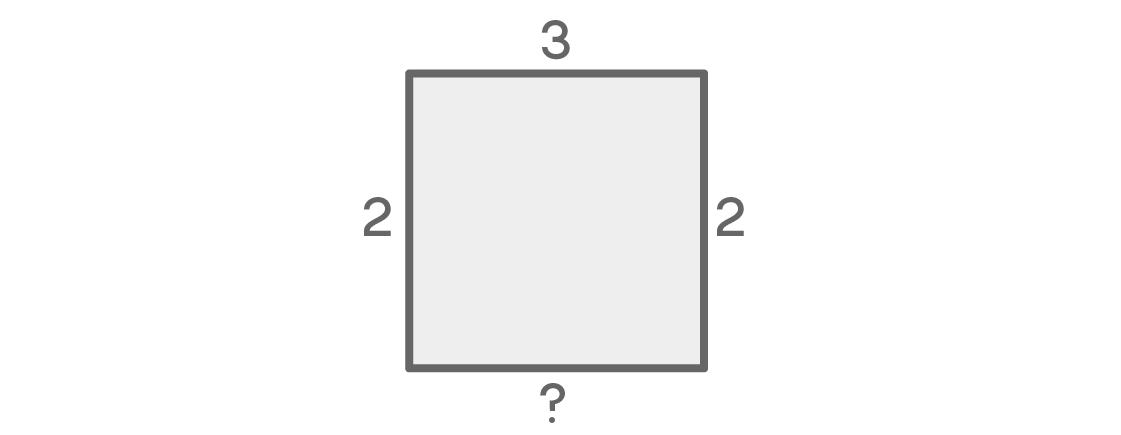
如果左右两边位置颜色不同，那下面的位置确实只有一种选择。例如，左边是蓝色的，右边是红色的，那么底下的就必须是黄色的。但是左右的颜色相同又会怎么样？在这种情况下，底下颜色的选择会有两种。最后的选择取决于一开始的选择，这就让我们的计算变得复杂起来。

因此我们必须考虑两种相互独立的情况：左边和右边颜色相同的时候和左边和右边颜色不相同的时候。

如果左边和右边的颜色相同，那么每条边颜色的可能性就如下图所示：

 

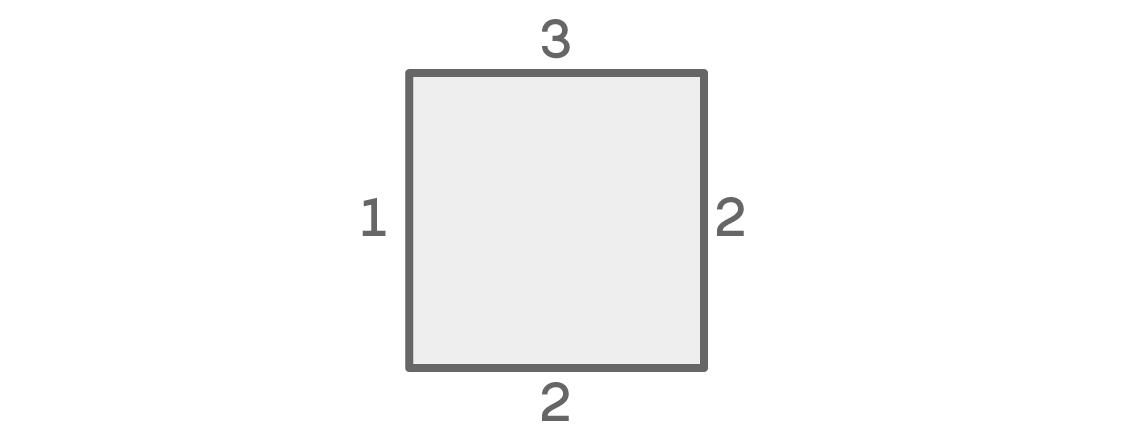
首先，上面的颜色有三种选择。然后，对于右边的颜色还剩了两种选择。因为我们假设左边和右边颜色是一样的，所以左边的颜色只有一种可能：和右边的颜色相同。最后，因为左边和右边颜色相同，底下的颜色可以是剩下的两种颜色中的任意一种。这样我们就有  3 × 2 × 1 × 2 = 12种可能的结果。

现在让我们考虑一下左边和右边颜色不同时的可能性：

 

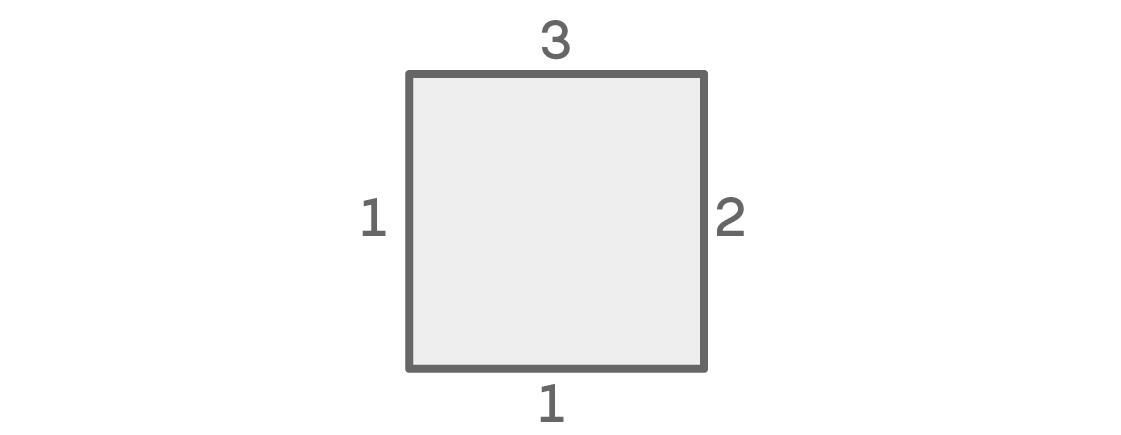
同样，上面有三种选择右边有两种选择。左边仍然只有一种选择，但是这次的原因和第一次的不同： 它既不能和相邻的上面颜色相同，又得符合假设和右边颜色不同。而因为左边和右边的颜色不同，下面的颜色只有一种选择（和上面一样的颜色）。这种情况有3 × 2 × 1 × 1 = 6种可能的结果。

因为这两种情况包含了所有的可能，我们只需要把它们加起来得到总共有12 + 6 = 18种可能的结果。

增加了一种颜色让我们的问题变得复杂，但是我们的努力会得到回报。我们现在可以用这种方法解决4，5或者任意q种不同颜色时的问题。

无论在多少种颜色中进行选择，我们都要考虑两种情况：左边和右边颜色相同，左边和右边颜色不同。假设我们需要在q种不同的颜色种进行选择。下面的图像表示的是当左右颜色相同时每条边不同的选择数量：

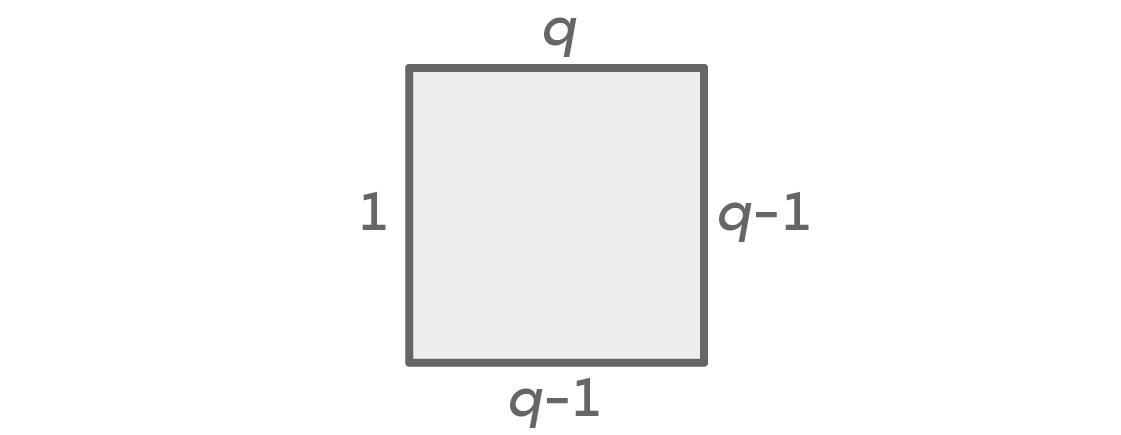
一开始，上面的座位有q种颜色可以选择，右面的座位有q-1种颜色可以选择。因为我们假设左边和右边颜色相同，所以左边只有一种选择。这样，下面可以选择q-1种颜色，即除了左右的那种颜色之外的任何颜色。根据基本算数原理我们一共得到了q × (q – 1) × 1 × (q – 1) = q(q – 1)²种可能的结果。

如果左右颜色不同，我们可以像这样列举可能的结果：

 

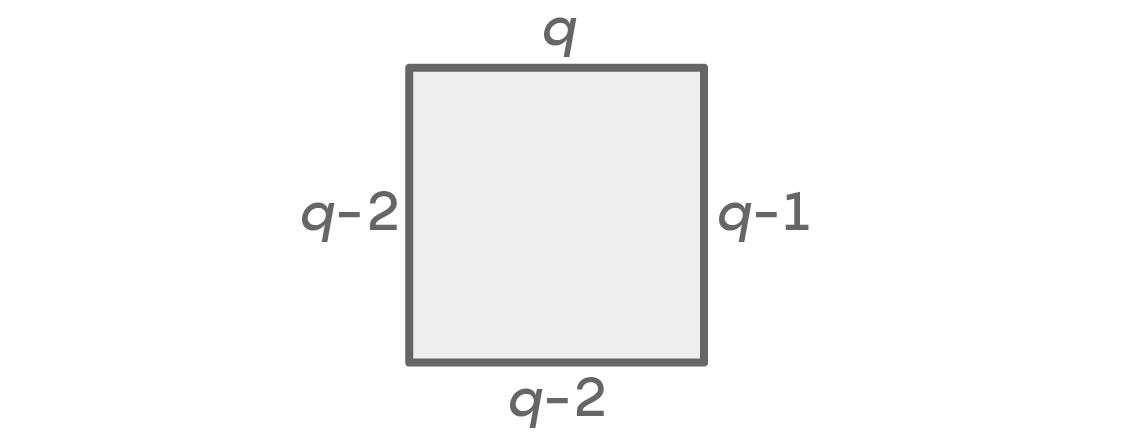
同样，上面的座位有q种颜色可以选择，右边的座位有q种颜色可以选择。现在，左边的颜色不能和右边的颜色相同，所以我们有q-2种选择。底下座位可以是除了左右两种不同颜色之外的任意颜色，同样也是有q-2种不同的颜色。这样我们一共有q × (q – 1) × (q – 2) × (q – 2) = q(q – 1)(q – 2)²种可能的结果。因为这两种情况包括了所有的可能性，我们像前面一样把它们加在一起得到最后可能结果的总数：q(q – 1)²+ q(q – 1)(q – 2)²。

这个表达式看起来好像和“我们能有多少种不同的方式让不同的队坐在方桌上，同时不让两个队友坐在一起”这个问题毫无关系。但是这个多项式表达了关于这个问题的好多信息。它不单告诉了我们具体的数字结果，还表现出隐藏在这道题之下的一些结构。

这个特别的多项式被称为“染色多项式”(chromatic polynomial)，因为它回答了下述问题：你有多少种不同的方法能够给网格（或图）的方格或者节点上色使其与相邻的方格或节点颜色不同。

我们的问题最初是关于给队伍在一张桌子上安排座位，但是我们可以很容易地把它转化成一个关于给图像上节点上色的问题。我们不再想象人们围着桌子坐，我们将人们比作节点，如果他们坐在一起就用一条线把他们连接起来。

 

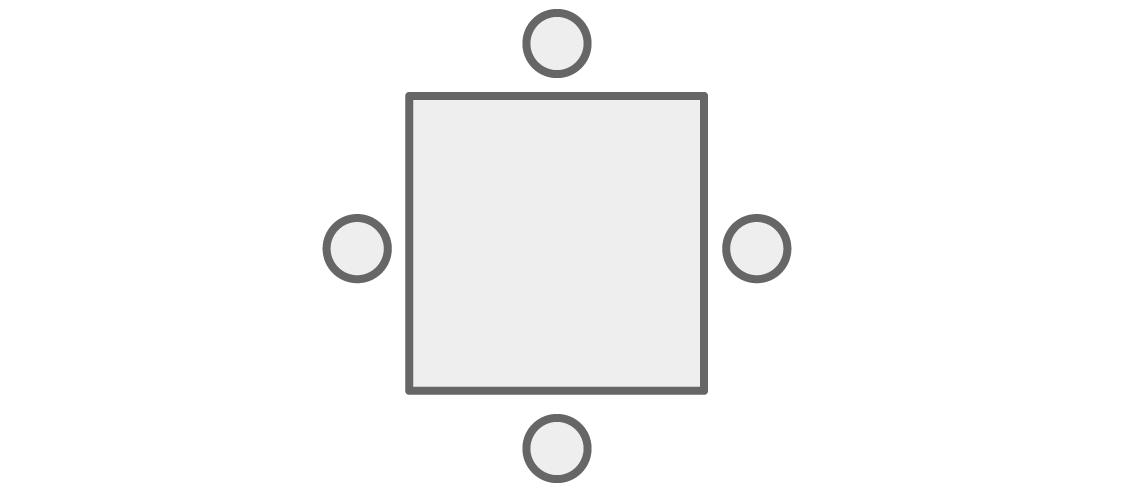
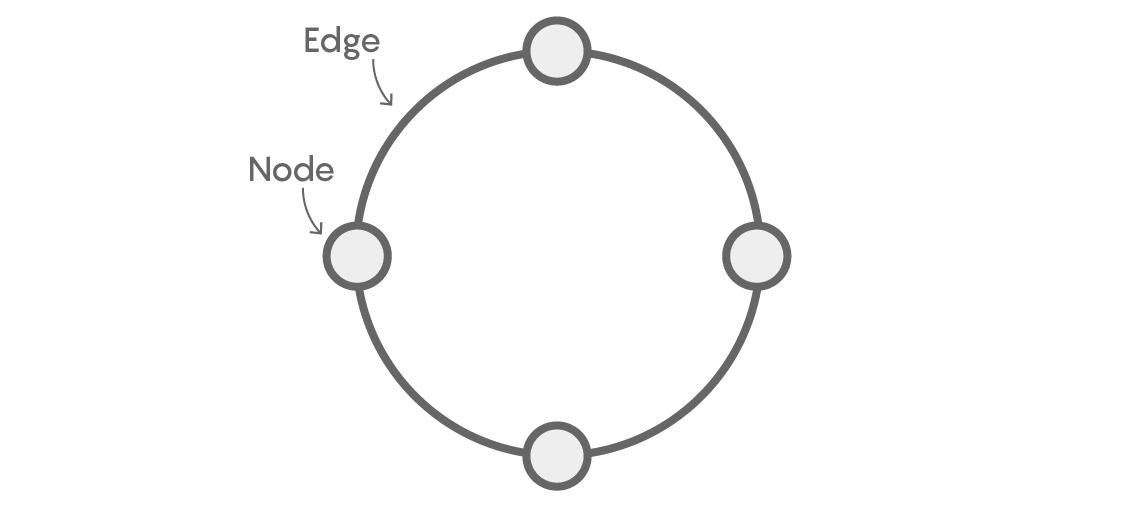
现在，图像中的每一个节点的颜色可以被看成方桌周围的一个座位，而“邻座”在图上变成了“有一条线段将它们连接起来” 。

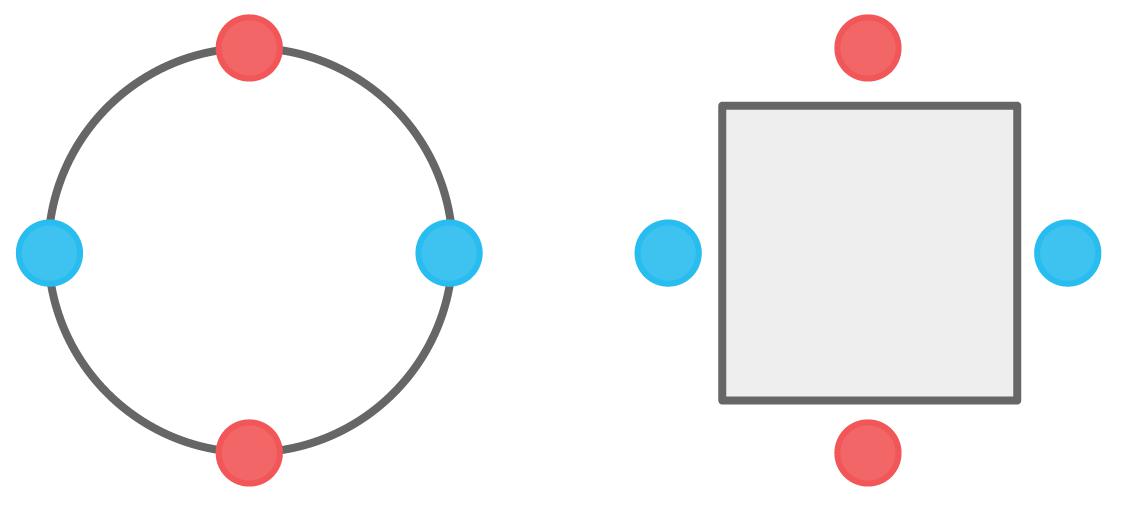
既然我们已经将我们的问题用一个图表示出来，那么让我们回到它的染色不等式。以下我们将成它为P(q)。

P(q) = q(q – 1)² + q(q – 1)(q – 2)²

这个多项式的好处是它能够回答我们所有可能的图像上色问题。

例如：为了得到有三个颜色的题的答案，我们让q=3，从而得到：

P(3) = 3(3 – 1)²+ 3(3 – 1)(3 – 2)²= 3 × 2² + 3 × 2 × 1² = 12 + 6 = 18

这个恰恰是在我们上面的三个队伍的情况下找到的答案。而当我们让q=2时：

P(2) = 2(2 – 1)² + 2(2 – 1)(2 – 2)² = 2 × 1²+ 2 × 1 × 0² = 2 + 0 = 2

看起来是不是很熟悉？这是我们一开始两个不同队伍的情况下时的答案。我们只需要给q代入适当的值就能够得到有四个，五个甚至是十个不同队伍情况下的答案：P(4) = 84, P(5) = 260 and P(10) = 6,570。色多项式通过归纳我们的算数方法，已经捕捉到了这个问题的一些基础结构。

我们可以通过对多项式P(q)做一些基本的代数运算揭露更多的结构

P(q) = q(q – 1)² + q(q – 1)(q – 2)²:

=q(q−1)(q−1)+q(q−1)(q−2)²

=q(q−1)((q−1)+(q−2)²)

=q(q−1)(q−1+q²−4q+4)

=q(q−1)(q²−3q+3)

这里我们已经把q(q – 1)从和中的每一个部分提取了出来然后合并同类项，把多项式变成用乘积表示出来的“因子形式”。在因子形式中，一个多项式可以通过它的“根”来告诉我们结构。

一个多项式的跟指的是使得多项式为0的去值。并且一个多项式的因子形式使得求根变得容易：因为多项式是以因式乘积的形式存在的，任何让其中一个因子为零都会让整个乘积变为零，因此多项式也是0。

例如，我们的多项式P(q) = q(q – 1)(q² – 3q + 3)有一个因子(q – 1)。如果我们让q=1，这个因式就变成了0，从而将整个式子变成了0。就是P(1) = 1(1 – 1)(1² – 3 × 1 + 3) = 1 × 0 × 1 = 0. Similarly, P(0) = 0 × (–1) × 3 = 0。所以q=1和q=0就是我们多项式的两个根。（你也许在考虑(q² – 3q + 3)的问题。因为没有一个实数能让这个因式变为0，所以它没有给我们的色多项式提供任何实根。）

这些代数根在我们的图像中是有意义的。如果我们只能选择一种颜色，那么每一个节点都会是相同的颜色。那么由于相邻的两个节点不能是相同的颜色，我们无法给这个图像上色。但是这就是q = 1是这个色多项式的根的含义。如果P(1) = 0，那么就没有办法能在给图像上色的同时保证相邻的节点颜色不同。如果我们有0种颜色供我们选择： P(0) = 0，结果也是同样的。染色多项式的根告诉了我们图的结构。

当我们开始看其他图像的时候，从代数的角度看这个结构的能力就变得更加重要了。让我们来看看下面的三角图像。

 

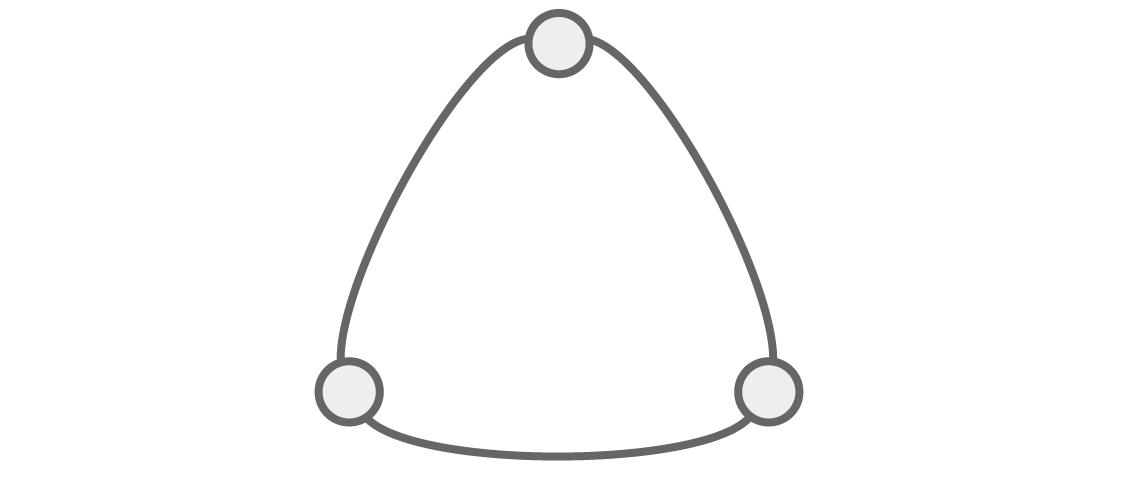
用q种颜色给上面的图像上色有多少种方法可以使任何相邻的两个节点颜色不同？

通常，前两个节点有分别有q和q-1种选择。因为剩下的节点是和前两个都相邻的，所以它的颜色必须和前两个的颜色都不相同，就只剩下了q-2种选择。所以这个三角图像对应的色多项式就是：P(q) = q(q – 1)(q – 2)。

在它的因式形式中，这个色多项式告诉了我们一些有趣的事情：q=2是一个根。而且如果P(2) = 0，我们无法用两种颜色给这个图像上色的同时保证相邻的两个节点颜色不同。

那么，想象一下沿着这个三角形的循环走，你每走到一个节点，就给它涂上颜色。因为你只有两种颜色可以选择，那你只能每走到一个节点就变换一种颜色：如果第一个是红色，那么第二个就必须是蓝色，这也代表着第三个必须是红色。但是第一个和第三个是相邻的，所以它们不能都是红色的。正如多项式预测的一样，两种颜色是不够的。

使用这种方法交替论证，你可以推导出一个有力的结论：任何有奇数个节点的循环的色多项式都必须有2作为一个根。这是因为如果你在一个有奇数个节点的循环中交替使用两种颜色，你就会给第一个和最后一个涂上一样的颜色。但是因为它是一个循环，第一个和最后一个是相邻的。这就是不可能满足条件的了。

例如，我们可以用各种技巧确定一个有五个节点的循环所对应的色多项式为P(q) = q⁵ – 5q⁴ + 10q³ – 10q² + 4q。但当我们把它变换为因式形式的时候，它就变成了P(q) = q(q – 1)(q – 2)(q² – 2q + 2)。就像我们猜测的那样，我们看见q = 2是一个根也就是P(2) = 0。值得注意的是，一旦我们建立起了图像和对应的多项式之间的联系，我们就会发现：多项式可以告诉我们图的结构，图也可以告诉我们它们所对应的多项式的结构。

正是对结构的研究让June Huh证明了Read在40年前关于染色多项式的猜想。这个猜想是说当我们按顺序列出一个色多项式的系数并且忽略它们的符号的时候，就满足了一个特殊情况：也就是，任何一个系数的平方都必然大于等于与它相邻的两个系数的乘积。例如：在有五个节点的循环所对应的色多项式中，P(q)  = q^5 -5q^4 +10q³- 10q² +4q，我们可以发现5² ≥ 1 × 10, 10² ≥ 5 × 10以及 10² ≥ 10 × 4。这说明并不是每一个多项式都是一个色多项式：染色多项式通过和图像的连接有着更深的结构。更重要的是，这些多项式和其他领域直接的关系让Huh和他的合作者在证明了Read的猜想几年后解决了一个更加广泛的开放性问题——罗塔猜想(Rota)。

大家都知道多项式没啥了不起的：不过就是用符号来抽象表示的一些运算而已。但是多项式以及多项式的特征——它们的根，它们的系数，它们各种各样的形式——能够帮助我们在令人惊奇的地方揭示结构，建立了我们日常生活和代数之间的联系。